¿Qué es la teoría de juegos?
Evidentemente definir la Teoría de Juegos es tan absurda como su lógica, pero la realidad es que la Teoría de Juegos consiste en razonamientos circulares, los cuales no pueden ser evitados al considerar cuestiones estratégicas. Por naturaleza, a los humanos no se les da muy bien pensar sobre los problemas de las relaciones estratégicas, pues generalmente la solución es la lógica a la inversa.
En la Teoría de Juegos la intuición no educada no es muy fiable en situaciones estratégicas, razón por la que se debe entrenar tomando en consideración ejemplos instructivos, sin necesidad que los mismos sean reales. Por lo contrario en muchas ocasiones disfrutaremos de ventajas sustanciales estudiando juegos, si se eligen cuidadosamente los mismos. En estos juegos-juegos, se pueden desentender de todos los detalles.
Si en lugar de utilizar personajes ficticios utilizamos personajes reales para los juegos si se observase qué tan honesto es ese personaje, cómo manipularía la información obtenida, etc. Para un especialista en Teoría de Juegos el ser deshonesto, etc., sería un error comparable al de un matemático que no respeta las leyes de la aritmética porque no le gustan los resultados que está obteniendo.
Si en lugar de utilizar personajes ficticios utilizamos personajes reales para los juegos si se observase qué tan honesto es ese personaje, cómo manipularía la información obtenida, etc. Para un especialista en Teoría de Juegos el ser deshonesto, etc., sería un error comparable al de un matemático que no respeta las leyes de la aritmética porque no le gustan los resultados que está obteniendo.
INTRODUCCIÓN A LA TEORÍA DE JUEGOS.
Los psicólogos destacan la importancia del juego en la infancia como medio de formar la personalidad y de aprender de forma experimental a relacionarse en sociedad, a resolver problemas y situaciones conflictivas. Todos los juegos,de niños y de adultos, juegos de mesa o juegos deportivos, son modelos de situaciones conflictivas y cooperativas en las que podemos reconocer situaciones y pautas que se repiten con frecuencia en el mundo real.
El estudio de los juegos ha inspirado a científicos de todos los tiempos para el desarrollo de teorías y modelos matemáticos. La estadística es una rama de las matemáticas que surgió precisamente de los cálculos para diseñar estrategias vencedoras en juegos de azar. Conceptos tales como probabilidad, media ponderada y distribución o desviación estándar, son términos acuñados por la estadística matemática y que tienen aplicación en el análisis de juegos de azar o en las frecuentes situaciones sociales y económicas en las que hay que adoptar decisiones y asumir riesgos ante componentes aleatorios.
Pero la teoría de juegos tiene una relación muy lejana con la estadística. Su objetivo no es el análisis del azar o de los elementos aleatorios sino de los comportamientos estratégicos de los jugadores. En el mundo real, tanto en las relaciones económicas como en las políticas o sociales, son muy frecuentes las situaciones en las que, al igual que en los juegos, su resultado depende de la conjunción de decisiones de diferentes agentes o jugadores. Se dice de un comportamiento que es estratégico cuando se adopta teniendo en cuenta la influencia conjunta sobre el resultado propio y ajeno de las decisiones propias y ajenas.
La técnica para el análisis de estas situaciones fue puesta a punto por un matemático, John von Neumann. A comienzos de la década de 1940 trabajó con el economista Oskar Morgenstern en las aplicaciones económicas de esa teoría. El libro que publicaron en 1944, "Theory of Games and Economic Behavior", abrió un insospechadamente amplio campo de estudio en el que actualmente trabajan miles de especialistas de todo el mundo.
La Teoría de Juegos ha alcanzado un alto grado de sofisticación matemática y ha mostrado una gran versatilidad en la resolución de problemas. Muchos campos de la Economía —Equilibrio General, distribución de costes, etc.— se han visto beneficiados por las aportaciones de este método de análisis. En el medio siglo transcurrido desde su primera formulación el número de científicos dedicados a su desarrollo no ha cesado de crecer. Y no son sólo economistas y matemáticos sino sociólogos, politólogos, biólogos o psicólogos. Existen también aplicaciones jurídicas: asignación de responsabilidades, adopción de decisiones de pleitear o conciliación, etc.
Hay dos clases de juegos que plantean una problemática muy diferente y requieren una forma de análisis distinta. Si los jugadores pueden comunicarse entre ellos y negociar los resultados se tratará de juegos con transferencia de utilidad (también llamados juegos cooperativos), en los que la problemática se concentra en el análisis de las posibles coaliciones y su estabilidad. En los juegos sin transferencia de utilidad, (también llamados juegos no cooperativos) los jugadores no pueden llegar a acuerdos previos; es el caso de los juegos conocidos como "la guerra de los sexos", el "dilema del prisionero" o el modelo "halcón-paloma".
Los modelos de juegos sin transferencia de utilidad suelen ser bipersonales, es decir, con sólo dos jugadores. Pueden ser simétricos o asimétricos según que los resultados sean idénticos desde el punto de vista de cada jugador. Pueden ser de suma cero, cuando el aumento en las ganancias de un jugador implica una disminución por igual cuantía en las del otro, o de suma no nula en caso contrario, es decir, cuando la suma de las ganancias de los jugadores puede aumentar o disminuir en función de sus decisiones. Cada jugador puede tener opción sólo a dos estrategias, en los juegos biestratégicos, o a muchas. Las estrategias pueden ser puras o mixtas; éstas consisten en asignar a cada estrategia pura una probabilidad dada. En el caso de los juegos con repetición, los que se juegan varias veces seguidas por los mismos jugadores, las estrategias pueden ser también simples o reactivas, si la decisión depende del comportamiento que haya manifestado el contrincante en jugadas anteriores.
Ejemplo: Piedra, papel, tijera
Piedra vence a las tijeras rompiéndolas, las tijeras vencen al papel cortándolo, y el papel vence a la piedra envolviéndola.
Cada entrada +1 indica una ganancia para el jugador renglón, -1 indica una pérdida, y 0 indica un empate.
¿Quiere jugar? Clic en una acción renglón...
Estrategia mixta, Valor esperado
Un jugador usa una estrategia pura si usa la misma acción a cada turno del juego. El jugador usa una estrategia mixta si a cada turno escoge al azar un acción para que cada acción se está usado una fracción determinada del tiempo.
Representamos una estrategia mixta (o pura) del jugador reglón por una matriz con un solo renglón (vector probabilidad):
R = [a b c . . . ]con lo mismo número de entradas que renglones, y en cual cada entrada representa la fracción de tiempo que está usada la correspondiente acción (o la probabilidad de usar aquel acción) y donde a + b + . . . = 1.
Una estrategia mixta para el jugador renglón se represente por un vector probabilidad similar, pero en forma de columna C. Para ambos jugadores, estrategias puras son representadas por vectores probabilidad con un solo 1 y el resto de las entradas 0.
El valor esperado del juego con matriz de pagos P que resulta por las estrategias mixtasR y C es dado por
e = RPCEl valor esperado del juego es el pago promedio por turno si cada jugador usa su estrategia mixta especificado por R y C después de un gran número de turnos.
ejemplo
Aquí es una variante de "piedra, papel, tijera" en la que "papel/papel" y "piedra/piedra" ya no está un empate.
 |  |  | |||
 |  |  | |||
 | |||||
 |
Suponga el jugador de renglón usa la estrategia mixta
R = [0.75 0 0.25](juega papel 75% del tiempo, tijeras 0% del tiempo y piedra 25% del tiempo) y el jugador columna juega tijeras y piedra 50% del tiempo cada uno;
Entonces el valor esperado del juego es
C =
0
0.5
0.5 .
| e | = RPC | |||||||
| = [0.75 0 0.25] |  |  |  | 0 |  | |||
| 0.5 | ||||||||
| 0.5 | ||||||||
| = -0.125 |
Criterio minimax, Principios fundamentales de la teoría de juegos
Criterio Minimax Un jugador quien usa el criterio minimax escoge una estrategia que, entre todas las estrategias posibles, minimiza el daño de la mejor contra-estrategia del otro jugador. Es decir, una estrategia óptima según el criterio minimax es una que minimiza el daño máximo que puede hacer el contrincante.
Encontrar la estrategia se llama solucionar el juego
Principios fundamentales de la teoría de juegos Cuando analizamos cualquier juego, hacemos los siguientes supuestos acerca de los dos jugadores:
- Cada jugador hace la acción mejor posible.
- Cada jugador sabe que su contrincante está también haciendo la acción mejor posible.
Ejemplo
Considere el siguiente juego:
| Acción Columna | ||||||
| A | B | C | ||||
| Acción Renglón | 1 |  |  | |||
| 2 | ||||||
| 3 | ||||||
Si el jugador renglón sigue Principio 1, nunca debería jugar Acción 1 pues Acción 2 da mejor pagos sin tener en cuenta cual acción escoja el jugador columna. (Los pagos en renglón 2 son por lo menos tan altos que los pagos correspondientes en renglón 1.)
Además, siguiendo Principio 2, el jugador renglón espera que el jugador columna nunca jugaría Acción A, pues Acción B da mejor pagos desde el punto de vista del jugador columna. (Los pagos en columna B son por lo menos tan bajos que los pagos correspondientes en columna A.)
Reducir por predominio
Una acción domina a otra si todos sus pagos son por lo menos tan provechoso al jugador que los pagos correspondientes de la otra. En términos de la matriz de pagos, podemos decirlo como sigue:
- Renglón r en la matriz de pagos domina a renglón s si cada pago en renglón r ≥ el pago correspondiente en renglón s.
- Columna r en la matriz de pagos domina a columna s si cada pago en columna r ≤ el pago correspondiente en columna s.
Siguiendo el primero principios de la teoría de juegos, la acción que corresponde a un renglón o columna estrictamente dominado nunca será jugado, y ambos jugadores son conscientes de esto por el segundo principio. Entonces cada jugador quien sigue los principios de la teoría de juegos eliminará repetidamente renglones y columnas dominadas como podría ser el caso. (En el caso que son iguales dos renglones o columnas, no hay razón para elegir uno sobre el otro, entonces cualquiera de los dos puede ser eliminado.) Este proceso se llama reducción por predominio.
Ejemplo
Considere otra vez el siguiente juego.
| Acción Columna | ||||||
| A | B | C | ||||
| Acción Renglón | 1 |  |  | |||
| 2 | ||||||
| 3 | ||||||
Pues las entradas de Renglón 2 son ≥ las entradas correspondientes en Renglón 1, entonces Renglón 2 domina a Renglón 1.
Pues las entradas de Columna B son ≤ las entradas correspondientes en Columna A, Columna B domina a Columna A.
Reducir el juego más arriba por predominio
Pues Renglón 2 domina a Renglón 1, eliminamos Renglón 1 para obtener
| A | B | C | |||
| 2 |  |  | |||
| 3 |
Pues Columna B ahora domina a ambas Columnas A y C, eliminamos las dos Columnas A y C para obtener
| B | |||
| 2 |  |  | |
| 3 |
Pues el primero renglón domina ahora al último renglón, eliminamos el último renglón, y estamos reducidos a la siguiente matriz 1×1
| B | |||
| 2 | ( | ) |
En este caso, hemos solucionado el juego por reducción por predominio: El jugador renglón debe siempre jugar 2 y el jugador de columna debe siempre jugar B. Pues el pago correspondiente es 0, decimos que el juego es justo (ninguno jugador tiene ventaja sobre el otro).
Observe que tuvimos suerte aquí: No todos los juegos pueden ser reducido a un juego 1×1 por predominio.
Punto de silla, juego estrictamente determinadoUn punto de silla es un pago que es simultáneamente un mínimo de su renglón y un máximo de su columna. Para encontrar puntos de silla, Encierre en círculo los mínimos de todos los renglones y meta en caja los máximas de todas las columnas. Los puntos de silla son aquellas entradas que son simultáneamente en círculo y en caja.Un juego es estrictamente determinado si tiene por lo menos uno punto de silla. Las siguientes declaraciones se aplican a los juegos estrictamente determinado:- Todos los puntos de silla en un juego tienen los mismos valores de pago.
- Elegir el renglón y la columna que pasan por cualquier punto de silla de estrategias minimax para ambos jugadores. Es decir, el juego es solucionado por el uso de estas estrategias puras.
El valor de un juego estrictamente determinado es el valor del punto de silla. Un juegojusto tiene un valor igual a cero, si no, es injusto o parcial.
EjemploEn el juego más arriba, hay dos puntos de silla, mostrados en color.
A B C 1 
0
-1
1 
2
0
0
2 3
-1
-2
3
| A | B | C | |||
| 1 |  |  | |||
| 2 | |||||
| 3 |
Juegos
Se denomina juego a la situación interactiva especificada por el conjunto de participantes, los posibles cursos de acción que puede seguir cada participante, y el conjunto de utilidades.
Estrategia
Cuando un jugador tiene en cuenta las reacciones de otros jugadores para realizar su elección, se dice que el jugador tiene una estrategia. Una estrategia es un plan de acciones completo que se lleva a cabo cuando se juega el juego. Se explicita antes de que comience el juego, y prescribe cada decisión que los agentes deben tomar durante el transcurso del juego, dada la información disponible para el agente. La estrategia puede incluir movimientos aleatorios.
Resultados de los juegos
El resultado de un juego es una cierta asignación de utilidades finales. Se denomina resultado de equilibrio si ningún jugador puede mejorar su utilidad unilateralmente dado que los otros jugadores se mantienen en sus estrategias. Un equilibrio estratégico es aquel que se obtiene cuando, dado que cada jugador se mantiene en su estrategia, ningún jugador puede mejorar su utilidad cambiando de estrategia. Alternativamente, un perfil de estrategias conforma un equilibrio si las estrategias conforman la mejor respuesta a las otras.
Forma normal versus forma extensiva de los juegos
En juegos de forma normal, los jugadores mueven simultáneamente. Si el conjunto de estrategias es discreto y finito, el juego puede ser representado por una matriz NxM (ver abajo). Un juego en forma extensiva especifica el orden completo de movimientos a través de la dirección del juego, generalmente en un árbol de juego.
Juegos NxM
Una forma de juegos de dos jugadores, en la cual un jugador tiene N acciones posibles y el otro tiene M acciones posibles. En un juego así, los pares de utilidades o pagos pueden ser representados en una matriz y el juego es fácilmente analizable. Los juegos NxM dan una idea de cómo puede verse la estructura de un juego mas complejo.
Matriz de resultados de un juego
La matriz de resultados de un juego representa el resultado del juego en una matriz. Supongamos que dos personas, A y B, están jugando un sencillo juego. El juego consiste en lo siguiente: la persona A tiene la posibilidad de elegir “arriba” o “abajo”, mientras que B puede elegir “izquierda” o “derecha”. Los resultados del juego se representan en la matriz de resultados:
Izquierda | Derecha | |
Arriba | (50 , 100) | (0 , 50) |
Abajo | (100 , 50) | (50 , 0) |
Estrategia dominante
Una estrategia dominante es aquella elección que realiza el jugador independientemente de lo que haga el otro. En el juego representado en la matriz de arriba, la estrategia dominante para A es elegir “abajo”, mientras que la estrategia dominante para B es elegir “izquierda”. Estas estrategias dominantes dan como resultado el equilibrio de estrategias dominantes del juego. Si cada jugador tiene una estrategia dominante se puede predecir el resultado del juego.
Equilibrio de Nash
El equilibrio de Nash fue formulado por John Nash, que es un matemático norteamericano, en 1951. Un par de estrategias es un equilibrio de Nash si la elección de A es óptima dada la de B y la de B es óptima, dada la de A. El equilibrio de Nash se diferencia del equilibrio de las estrategias dominantes en que, en el equilibrio de las estrategias dominantes, se exige que la estrategia de A sea óptima en el caso de todas las elecciones óptimas de B, y viceversa. El equilibrio de Nash es menos restrictivo que el equilibrio de estrategias óptimas.
Un juego puede tener más de un equilibrio de Nash. Existen juegos en los no existe un equilibrio de Nash.
Dilema del prisionero
Considera la siguiente historia. Dos sospechosos de un crimen son puestos en celdas separadas. Si ambos confiesan, cada uno será sentenciado a tres años de prisión. Si sólo uno confiesa, el que confiese será liberado y usado como testigo contra el otro, quien recibirá una pena de diez años. Si ninguno confiesa, ambos serán condenados por un cargo menor y tendrán que cumplir una pena de sólo un año de prisión. Este juego puede ser representado por una matriz 2x2:
Sospechoso B confiesa | Sospechoso B no confiesa | |
Sospechoso A confiesa | (3 , 3) | (0 , 10) |
Sospechoso A no confiesa | (10 , 0) | (1 , 1) |
Veamos cuál es la estrategia óptima para cada sospechoso. Si B confiesa, A preferirá confesar, ya que si confiesa obtendrá una pena de 3 años, y si no confiesa obtendrá una pena de 10 años. Si B no confiesa, A preferirá confesar, ya que de este modo será liberado, y si no confesara obtendrá una pena de un año. Entonces, A va a confesar, independientemente de lo que haga B. Análogamente, B también va a confesar independientemente de lo que haga A. Es decir, ambos sospechosos van a confesar y obtener entonces una pena de tres años de prisión cada uno. Este es el equilibrio del juego, que es ineficiente en el sentido de Pareto, ya que se puede reducir la condena de ambos si ninguno confesara.
Este es el ejemplo mas famoso de las situaciones en la que los equilibrios competitivos pueden llevar a resultados ineficientes. El dilema del prisionero ilustra la situación que se presenta en los cárteles. En un cártel, las empresas coalicionan (hacen un acuerdo) para reducir su producción y así poder aumentar el precio. Sin embargo, cada empresa tiene incentivos para producir mas de lo que fijaba el acuerdo y de este modo obtener mayores beneficios. Sin embargo, si cada una de las firmas hace lo mismo, el precio va a disminuir, lo que resultará en menores beneficios para cada una de las firmas. La misma estructura de interacciones caracteriza el problema de la provisión de bienes públicos (problema del free rider), y del pago voluntario de impuestos.
Juegos de suma constante
Juegos en los que para cada combinación de estrategias, la suma de los pagos (o utilidades) a cada jugador es la misma. Todas las situaciones de intercambio que no permiten la creación o destrucción de recursos son juegos de suma constante.
Árbol de juegos
El árbol de juegos es una representación de un juego que describe la estructura temporal de un juego en forma extensiva. EL primer movimiento del juego se identifica con un nodo distintivo que se llama la raíz del juego. Una jugada consiste en una cadena conectada de ramas que comienza en la raíz del árbol y termina, si el juego es finito, en el nodo terminal. Los nodos representan los posibles movimientos en el juego. Las ramas que parten de los nodos representan las elecciones o acciones disponibles en cada movimiento. A cada nodo distinto del nodo terminal se le asigna el nombre de un jugador de modo que se sabe quién hace la elección en cada movimiento. Cada nodo terminal informa sobre las consecuencias para cada jugador si el juego termina en ese nodo.
Juego repetido
En un juego repetido un grupo fijo de jugadores juega un juego dado repetidamente, observando el resultado de todas las jugadas pasadas antes que comience la siguiente jugada. La posibilidad de observar las acciones y los resultados pasados antes de que comience la siguiente jugada permite que los jugadores penen o premien las acciones pasadas, de modo que surgen estrategias que no surgirían en los juegos simples no repetidos. Por ejemplo, repitiendo el juego del dilema del prisionero un número suficiente de veces da como resultado un equilibrio en el cual ambos prisioneros nunca confiesan.
Tipos de Juego según la suma de los resultados
Juegos de Suma Cero
En los juegos de suma cero, la suma de los pagos que reciben cada uno de los jugadores al final del juego es cero, debido a que los pagos positivos se compensan con los pagos negativos, o bien todos los pagos son cero.
Ejemplo:
| B: izquierda | B: derecha | |
| A: arriba | (0,0) | (1,-1) |
| A: abajo | (-1,1) | (0,0) |
En este ejemplo hay dos jugadores A y B, A puede elegir arriba o abajo mientras que B puede elegir izquierda o derecha. Los vectores representan los pagos que recibirá cada uno de acuerdo a su elección y a la elección del otro jugador. En este caso, A elegirá arriba y B elegirá izquierda ( ¿Porqué? ) y obtendrán como resultado cero cada uno.
Juegos de Suma Constante
Los juegos de suma constante son juegos en los que para cada combinación de estrategias, la suma de los pagos (o utilidades) a cada jugador es la misma. Todas las situaciones de intercambio que no permiten la creación o destrucción de recursos son juegos de suma constante.
| B: izquierda | B: derecha | |
| A: arriba | (1,1) | (0,2) |
| A: abajo | (2,0) | (1,1) |
En este caso A elegirá abajo mientras que B elegirá derecha ( ¿Porqué? ). Como resultado ambos participantes obtendrán 1.
Tipos de Juego según la Cantidad de Participantes
En las situaciones de juegos unipersonales no existen conflictos de intereses, sólo el interés del jugador individual. Los juegos individuales no son objeto de la teoría de juegos, pero pueden ser analizados teniendo en cuenta su complejidad y realizando un análisis probabilístico.
La mayoría de los problemas simples de la teoría de juegos están planteados como tipos de juegos bipersonales. Sin embargo estos se pueden extender a juegos de n personas. Esta extensión hace mas complicado el análisis, debido a que se multiplican las estrategias posibles, pero al mismo tiempo hacen la situación mas realista en algunos casos.
Tipos de Juegos según la cantidad de períodos
En los tipos de juego de un solo movimiento cada jugador tiene la posibilidad de elegir una sola vez, es decir, el tiempo se reduce a un único período. En los juegos recursivos o repetidos, el período de análisis está compuesto por varios períodos o incluso por infinitos períodos de tiempo. Generalmente los jugadores analizan las jugadas de los otros jugadores y reaccionan estratégicamente en el período siguiente, analizando las jugadas pasadas. Esto permite que los jugadores premien o penen a otros jugadores de acuerdo a sus jugadas pasadas. Los juegos recursivos son muy útiles para analizar muchas situaciones de la economía, por ejemplo una situación de duopolio puede ser analizada como un juego recursivo, en el cual si una empresa disminuye sus precios, en el período siguiente la otra responderá disminuyendo sus precios.
Tipos de Juego según su Forma
Juegos en forma extensiva (árbol)
Un juego en forma extensiva especifica el orden completo de movimientos a través de la dirección del juego, generalmente mediante un árbol de juego. Un árbol de juegos es una representación de un juego que describe la estructura temporal de un juego en forma extensiva.
Juegos en forma estratégica (normal)
Los jugadores mueven simultáneamente. Si el conjunto de estrategias es discreto y finito, este tipo de juego puede ser representado por una matriz de resultados..
Juegos en forma coalicional
Juegos en forma coalicional: un juego en forma coalicional se caracteriza por incluir la posibilidad de que exista un contrato que puede hacerse cumplir. Si los jugadores pueden comunicarse entre sí y negociar un contrato, las estrategias que surgen serán muy diferentes. El contrato puede incluir compensaciones entre jugadores, por ejemplo, si se conocen todos los resultados posible, la estrategia puede ser que los participantes elijan la situación óptima y luego repartan los beneficios entre todos los participantes.
| B:izquierda | B: derecha | |
| A:arriba | (10,0) | (10,0) |
| A:abajo | (0,0) | (0,200) |
En este caso la estrategia dominante de A es arriba, dado que obtendrá siempre 10 en vez de cero. Sin embargo, si A elije abajo y B derecha, B obtendrá 200, por lo que hay un margen de negociación para que B se comprometa a entregarle a A un monto a cambio de que A elija abajo. El monto puede estar entre 10 y 200.
La estrategia Maximín
juego de suma cero estrategias pago matriz de pagos punto de silla solución estable minimax estrategias mixtas teorema del minimax |
Consideremos un juego de suma cero en el que lo que yo gano lo pierde el otro jugador. Cada jugador dispone de tres estrategias posibles a las que designaremos como A, B, y C (supongamos que son tres tarjetas con dichas letras impresas). Los premios o pagos consisten en la distribución de diez monedas que se repartirán según las estrategias elegidas por ambos jugadores y se muestran en la siguiente tabla llamada matriz de pagos. Mis ganancias, los pagos que puedo recibir, se muestran en verde, a la izquierda de cada casilla. Los pagos al otro jugador se muestran en rosa, a la derecha de cada casilla. Para cualquier combinación de estrategias, los pagos de ambos jugadores suman diez.
MATRIZ DE PAGOS | ||||
| Las estrategias del otro jugador | ||||
| A | B | C | ||
Mi estrategia | A | 9 | 1 | 1 | 9 | 2 | 8 |
| B | 6 | 4 | 5 | 5 | 4 | 6 | |
| C | 7 | 3 | 8 | 2 | 3 | 7 | |
Por ejemplo. Si yo juego la tarjeta C y el otro jugador elige su tarjeta B entonces yo recibiré ocho monedas y el otro jugador recibirá dos.
Éste es por tanto un juego de suma cero. Se llama juego de suma cero aquél en el que lo que gana un jugador es exactamente igual a lo que pierde o deja de ganar el otro.
Para descubrir qué estrategia me conviene más vamos a analizar la matriz que indica mis pagos, la de fondo verde. Ignoro cuál es la estrategia (la tarjeta) que va a ser elegida por el otro jugador. Una forma de analizar el juego para tomar mi decisión consiste en mirar cuál es el mínimo resultado que puedo obtener con cada una de mis cartas. En la siguiente tabla se ha añadido una columna indicando mis resultados mínimos.
MATRIZ DE MIS PAGOS | |||||
| La estrategia del otro jugador | |||||
| A | B | C | mínimos | ||
Mi estrategia | A | 9 | 1 | 2 | 1 |
| B | 6 | 5 | 4 | 4 | |
| C | 7 | 8 | 3 | 3 | |
En efecto,
- Si yo elijo la tarjeta A, puedo obtener 9, 1 o 2, luego como mínimo obtendré un resultado de 1.
- Si elijo la tarjeta B, puedo obtener 6, 5 o 4, luego como mínimo obtendré 4.
- Si elijo la tarjeta C, puedo obtener 7, 8 o 3, luego como mínimo obtendré 3.
De todos esos posibles resultados mínimos, el que prefiero es 4 ya que es el máximo de los mínimos. La estrategia MAXIMIN consiste en elegir la tarjeta B ya que esa estrategia me garantiza que, como mínimo, obtendré4.
¿Podemos prever la estrategia del otro jugador? Supongamos que el otro jugador quiere elegir también su estrategia MAXIMIN. Mostramos ahora sólo los pagos asignados al otro jugador en los que destacamos el pago mínimo que puede obtener para cada una de sus estrategias. Subrayamos el máximo de los mínimos y su estrategia maximin.
MATRIZ DE PAGOS AL OTRO JUGADOR | ||||
| La estrategia del otro jugador | ||||
| A | B | C | ||
Mi estrategia | A | 1 | 9 | 8 |
| B | 4 | 5 | 6 | |
| C | 3 | 2 | 7 | |
| mínimos | 1 | 2 | 6 | |
En efecto,
- Si él elige A, su peor resultado sería si yo elijo A con lo que yo obtendría 9 y él 1.
- Si él elige B, su peor resultado sería si yo elijo C con lo que yo obtendría 8 y él 2.
- Si él elige C, su peor resultado sería si yo elijo B con lo que yo obtendría 4 y él 6.
Su estrategia MAXIMIN consiste por tanto en jugar la carta C con lo que se garantiza que, al menos, obtendrá 6.
Éste es un juego con solución estable. Ninguno de los jugadores siente la tentación de cambiar de estrategia. Supongamos que se empieza a repetir el juego una y otra vez. Yo jugaré siempre mi estrategia maximin (B) y el otro jugará siempre su estrategia maximin (C). Cada uno sabe lo que jugará el otro la siguiente vez. Ninguno estará tentado de cambiar su estrategia ya que el que decida cambiar su estrategia perderá.
Se llama punto de silla al resultado en el que coinciden las estrategias maximin de ambos jugadores.
No todos los juegos tienen un punto de silla, una solución estable. La estabilidad del juego anterior desaparece simplemente trastocando el orden de las casillas BB y BC:
MATRIZ DE MIS PAGOS | MATRIZ DE PAGOS AL OTRO JUGADOR | |||||||||
| La estrategia del otro jugador | La estrategia del otro jugador | |||||||||
| A | B | C | A | B | C | |||||
Mi estrategia | A | 9 | 1 | 2 | Mi estrategia | A | 1 | 9 | 8 | |
| B | 6 | 4 | 5 | B | 4 | 6 | 5 | |||
| C | 7 | 8 | 3 | C | 3 | 2 | 7 | |||
En esta nueva tabla mi estrategia maximin sigue siendo la B y la estrategia maximin del otro jugador sigue siendo la C. Pero la solución ahora ya no es estable. Si jugamos repetidas veces y yo repito mi estrategia maximín, B, el otro estará tentado de cambiar su estrategia, pasando de la C a la B con lo que obtendrá un pago mayor, 6 en vez de 5.
Claro que si el otro empieza a elegir sistemáticamente la estrategia B yo preferiré cambiar mi estrategia a la C para así obtener 8. Entonces el querrá volver a su estrategia C y así sucesivamente.
Realice ahora estos
Ejercicios MAXIMÍN
Ejercicios MAXIMÍN
Cuando se repiten juegos que no tienen solución estable interesa utilizar estrategias mixtas. Las estrategias mixtasconsisten en asignar a cada una de las estrategias una probabilidad. En el juego que estamos analizando una estrategia mixta podría describirse de la forma siguiente: "Para elegir la tarjeta que voy a jugar lanzaré un dado. Si el dado muestra un 1, elegiré la tarjeta A; si el dado muestra un 2 o un 3, elegiré la tarjeta B; si el dado muestra un 4, un 5 o un 6, elegiré la tarjeta C". En otras palabras, elegiré la tarjeta A con una probabilidad de 1/6, la tarjeta B con una probabilidad de 1/3 y la tarjeta C con una probabilidad de 1/2.
El teorema del maximin afirma que en todo juego bipersonal de suma cero en el que sea posible jugar estrategias mixtas además de las puras, las estrategias maximin de cada jugador coincidirán siempre en una solución estable, un punto de silla. Este teorema fue demostrado matemáticamente por John von Neumann en un artículo publicado en 1928.
La estrategia maximín página interactiva de ejercicios |
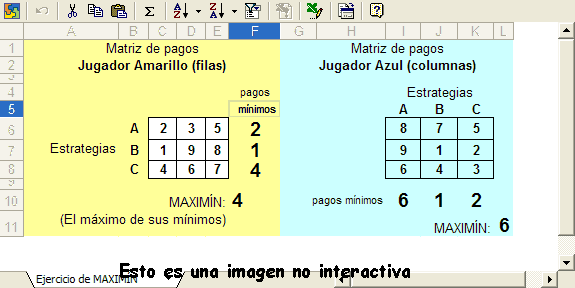
Este es un ejercicio interactivo. Bajo este párrafo debe aparecer un marco con una hoja de cálculo que permite modificar los valores de la matriz de pagos del jugador Amarillo y actualizará automáticamente los pagos del jugador Azul y los valores de pagos mínimos y maximín. Para poder visualizar correctamente el ejercicio, debe utilizar un navegador web con Javascript habilitado. Los que no puedan ver este marco, encontrarán al final de los ejercicios una imagen no interactiva del mismo.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Antes de empezar con los ejercicios responda:
- ¿Es éste es un juego de suma nula?
- ¿Porqué?
- ¿Qué ventajas tiene elegir la estrategia maximín?
Ejercicios
- Modificando solo los pagos del jugador amarillo, realice los cambios necesarios para obtener los siguientes resultados:
1-a) Consiga que el maximin de Amarillo sea 7
1-b) Consiga que el maximin de Azul sea 3
1-c) Consiga los dos resultados anteriores simultáneamente
1-d) Consiga el resultado c) cuando ambos jugadores eligen la estrategia C
1-e) Consiga el resultado d) manteniendo la característica de que todos los pagos de la matriz sean diferentes.
1-f) Consiga el resultado e) simplemente intercambiando la posición
de los pagos de cuatro casillas.
- Modificando solo los pagos del jugador amarillo, consiga que cuando Azul elija la estrategia A tenga garantizado obtener un pago de 14 o superior.
La toma de decisión y su puesta en práctica
Con frecuencia se pregunta si las organizaciones tienen normas y regulaciones relacionadas con un proceso por medio del cual un gerente puede llegar a alcanzar objetivos, políticas y estrategias.
Si bien no existe un conjunto de normas únicas para cualquiera de estas funciones, todas están relacionadas con diferentes formas de decisiones, por lo cual es posible elaborar una lista de pasos que se aplican a todas las circunstancias en las que se toman decisiones.
Podemos hablar entonces de un proceso básico conocido como el circuito o pasos de la toma de decisiones:
Si bien no existe un conjunto de normas únicas para cualquiera de estas funciones, todas están relacionadas con diferentes formas de decisiones, por lo cual es posible elaborar una lista de pasos que se aplican a todas las circunstancias en las que se toman decisiones.
Podemos hablar entonces de un proceso básico conocido como el circuito o pasos de la toma de decisiones:
Característica De La Decisión
Existen cinco características de las decisiones:
Existen cinco características de las decisiones:
- Efectos futuros:
- Tiene que ver con la medida en que los compromisos relacionados con la decisión afectará el futuro. Una decisión que tiene una influencia a largo plazo, puede ser considerada una decisión de alto nivel, mientras que una decisión con efectos a corto plazo puede ser tomada a un nivel muy inferior.
- Reversibilidad:Esta característica se refiere a la medida en que otras áreas o actividades se ven afectadas. Si el impacto es extensivo, es indicado tomar la decisión a un nivel alto; un impacto único se asocia con una decisión tomada a un nivel bajo.
- Impacto:Este factor se refiere a las relaciones laborales, valores éticos, consideraciones legales, principios básicos de conducta, imagen de la compañía, etc. Si muchos de estos factores están involucrados, se requiere tomar la decisión a un nivel alto; si solo algunos factores son relevantes, se recomienda tomar la decisión a un nivel bajo.
- Calidad:
- Periodicidad:
Este elemento responde a la pregunta de si una decisión se toma frecuente o excepcionalmente. Una decisión excepcional es una decisión de alto nivel, mientras que una decisión que se toma frecuentemente es una decisión de nivel bajo.
- Determinar la necesidad de una decisión:
- El proceso de toma de decisiones comienza con el reconocimiento de la necesidad de tomar una decisión, el mismo lo genera un problema o una disparidad entre cierto estado deseado y la condición real del momento.Una vez determinada la necesidad de tomar una decisión, se deben identificar los criterios que sean importantes para la misma. Vamos a considerar un ejemplo.
" Una persona piensa adquirir un automóvil , los criterios de decisión de un comprador típico serán: precio, modelo, dos o más puertas, tamaño nacional o importado, equipo opcional, color, etc. Estos criterios reflejan lo que el comprador piensa que es relevante. Existen personas para quienes es irrelevante que sea nuevo o usado; lo importante es que cumpla sus expectativas de marca, tamaño, imagen, etc., y se encuentre dentro del presupuesto del que disponen. Para el otro comprador lo realmente importante es que sea nuevo, despreciando el tamaño, marca, prestigio, etc" - Identificar los criterios de decisión:Los criterios enumerados en el paso previo no tienen mayor importancia. Es necesario ponderar cada uno de ellos y priorizar su importancia en la decisión.
Cuando el comprador del automóvil se pone a ponderar los criterios, da prioridad a lo que por su importancia condiciona completamente la decisión: precio y tamaño. Si el vehículo elegido tiene los demás criterios ( color, puerta, equipo opcional, etc.), pero rebasa el importe de lo que dispone para su adquisición o es de menor tamaño al que se precisa por el uso que se le va a dar, entonces nos encontramos con que los demás criterios son relevantes en base a otros de importancia trascendental. - Asignar peso a los criterios:Es la base de la toma de decisiones y no es más que desplegar las alternativas. El tomador de la decisión tiene que confeccionar una lista de todas las alternativas posibles y que podrían utilizarse para resolver el problema.
- Desarrollar todas las alternativas:Una vez identificadas las alternativas, el tomador de las decisiones tiene que evaluar de manera crítica cada una de ellas. Las ventajas y desventajas de cada alternativa resultan evidentes cuando son comparadas.
La evaluación de cada alternativa se efectua analizándola con respecto al criterio ponderado. - Evaluar las alternativas:
- Seleccionar la mejor alternativa ( Toma de decisiones):
Una vez seleccionada la mejor alternativa se llega al final del proceso de la toma de decisiones, en el proceso racional. Esta selección es bastante simple. El tomador de decisiones sálo tiene que escoger la alternativa que tuvo la calificación más alta en el paso número cinco. El ejemplo nos daría como resultado la compra de un Mercedes, con mínimas diferencias con otras marcas.
El tomador de decisiones debe ser totalmente objetivo y lógico a la hora de tomarlas, tiene que tener una meta clara y todas las acciones en el proceso de toma de decisiones llevan de manera consistente a la selección de aquellas alternativas que maximizarán la meta.
El tomador de decisiones debe ser totalmente objetivo y lógico a la hora de tomarlas, tiene que tener una meta clara y todas las acciones en el proceso de toma de decisiones llevan de manera consistente a la selección de aquellas alternativas que maximizarán la meta.
Tipos De Decisiones
Las decisiones, pueden estar divididas en dos categorías.
Las decisiones, pueden estar divididas en dos categorías.
- Decisión Programada:
- Son programadas en la medida que son repetitivas y rutinarias, así mismo en la medida que se ha desarrollado un método definitivo para podermanejarlas. Al estar el problema bien estructurado, el mando no tiene necesidad de pasar por el trabajo y gasto de realizar un proceso completo de decisión.
Estas decisiones programadas cuentan con unas guías o procedimientos ( pasos secuenciales para resolver un problema) , unas reglas que garanticen consistencias en las disciplinas y con un alto nivel de justicia , aparte de una política, que son las directrices para canalizar elpensamiento del mando en una dirección concreta. - Decisión no Programada:
"La reestructuración de una organización" o "cerrar una división no rentable", son ejemplos de decisiones no programadas, También "la creación de una estrategia de mercado para un nuevo producto".
Prácticamente todas las decisiones se toman en un ambiente de cierta incertidumbre. Sin embargo, el grado varía de una certeza relativa a una gran incertidumbre. En la toma de decisiones existen ciertos riesgos implícitos.
En una situación donde existe certeza, las personas están razonablemente seguras sobre lo que ocurrirá cuando tomen una decisión, cuentan coninformación que se considera confiable y se conocen las relaciones de causa y efecto.
Por otra parte en una situación de incertidumbre, las personas sólo tienen una base de datos muy deficiente. No saben si estos son o no confiables y tienen mucha inseguridad sobre los posibles cambios que pueda sufrir la situación. Más aún, no pueden evaluar las interacciones de las diferentesvariables, por ejemplo una empresa que decide ampliar sus operaciones a otro país quizás sepa poco sobre la cultura, las leyes, el ambiente económico y las políticas de esa nación. La situación política suele ser tan volátil que ni siquiera los expertos pueden predecir un posible cambio en las mismas.
En una situación de riesgo, quizás se cuente con información basada en hechos, pero la misma puede resultar incompleta. Para mejorar la toma de decisiones se puede estimar las probabilidades objetivas de un resultado, al utilizar, por ejemplo modelos matemáticos. Por otra parte se puede usar laprobabilidad subjetiva, basada en el juicio y la experiencia. Afortunadamente se cuenta con varias herramientas que ayudan a los administradores a tomar decisiones más eficaces.
En una situación donde existe certeza, las personas están razonablemente seguras sobre lo que ocurrirá cuando tomen una decisión, cuentan coninformación que se considera confiable y se conocen las relaciones de causa y efecto.
Por otra parte en una situación de incertidumbre, las personas sólo tienen una base de datos muy deficiente. No saben si estos son o no confiables y tienen mucha inseguridad sobre los posibles cambios que pueda sufrir la situación. Más aún, no pueden evaluar las interacciones de las diferentesvariables, por ejemplo una empresa que decide ampliar sus operaciones a otro país quizás sepa poco sobre la cultura, las leyes, el ambiente económico y las políticas de esa nación. La situación política suele ser tan volátil que ni siquiera los expertos pueden predecir un posible cambio en las mismas.
En una situación de riesgo, quizás se cuente con información basada en hechos, pero la misma puede resultar incompleta. Para mejorar la toma de decisiones se puede estimar las probabilidades objetivas de un resultado, al utilizar, por ejemplo modelos matemáticos. Por otra parte se puede usar laprobabilidad subjetiva, basada en el juicio y la experiencia. Afortunadamente se cuenta con varias herramientas que ayudan a los administradores a tomar decisiones más eficaces.
Distinguir las bases cuantitativas y cualitativas para la toma de decisiones
La gama de técnicas se extiende desde las corazonadas en un extremo hasta los análisis matemáticos complejos en el extremo opuesto.
Desde el punto de vista práctico no existe ni una técnica mejor ni una combinación que deba utilizarse en todas las circunstancia. La selección es individual y por lo general está dictada por los antecedentes y conocimientos del gerente y por los recursos disponibles.
La gama de técnicas se extiende desde las corazonadas en un extremo hasta los análisis matemáticos complejos en el extremo opuesto.
Desde el punto de vista práctico no existe ni una técnica mejor ni una combinación que deba utilizarse en todas las circunstancia. La selección es individual y por lo general está dictada por los antecedentes y conocimientos del gerente y por los recursos disponibles.
- Bases no cuantitativas:
- Los medios no cuantitativos son útiles, no solo para los problemas que se refieren a los objetivos, si no también para los problemas que tratan con los medios de alcanzar los objetivos.
En aplicación, las bases no cuantitativas son en alto grado personales, ampliamente conocidas y están consideradas por muchos como la manera natural de tomar una decisión; existen cuatro bases: intuición, hechos, experiencias y opiniones consideradas - Bases cuantitativas:
Esta es la habilidad de emplear técnicas presentadas como métodos cuantitativos o investigación de operaciones, como pueden ser la programaciónlineal, teoría de líneas de espera y modelos de inventarios. Esta herramienta ayuda a los mandos a tomar decisiones efectivas, pero es muy importante no olvidar que las habilidades cuantitativas no deben, ni pueden reemplazar al buen juicio, en el proceso de la toma de decisiones.
Disponen de numerosos medios diferentes que implican mediciones. El desarrollo y la aplicación de técnicas cuantitativas aumentaron a mediados de la década de 1940. Este impulso se debió principalmente al mejoramiento en las mediciones, a la disponibilidad de las computadoras, al interésincrementado en las matemáticas aplicadas y al deseo de métodos más lógicos para los problemas administrativos corrientes.
En su mayor parte cuando se emplean métodos cuantitativos para la toma de decisiones, el énfasis está en los medios, o en la mejor manera de alcanzar el objetivo estipulado.
El resultado final o meta por lo general es dado, por ejemplo como:
Disponen de numerosos medios diferentes que implican mediciones. El desarrollo y la aplicación de técnicas cuantitativas aumentaron a mediados de la década de 1940. Este impulso se debió principalmente al mejoramiento en las mediciones, a la disponibilidad de las computadoras, al interésincrementado en las matemáticas aplicadas y al deseo de métodos más lógicos para los problemas administrativos corrientes.
En su mayor parte cuando se emplean métodos cuantitativos para la toma de decisiones, el énfasis está en los medios, o en la mejor manera de alcanzar el objetivo estipulado.
El resultado final o meta por lo general es dado, por ejemplo como:
- Minimizar el costo para las actividades.
- Maximizar el rendimiento total para la compañía.
- Opiniones consideradas:
Esta base particular se distingue por el uso de la lógica detrás de la decisión lógica que es explicativa y que se deriva de un cuidadoso análisis de la situación, además existe cuantificación de la decisión tentativa. Para hacer esto se reúnen estadísticas y se relacionan las decisiones.
En este análisis nos involucramos con ciertas teorías o técnicas que a continuación nombraremos:
En este análisis nos involucramos con ciertas teorías o técnicas que a continuación nombraremos:
- Programación Lineal:
Es una técnica de decisión que ayuda a determinar la combinación óptima de recursos limitados para resolver problemas y alcanzar los objetivos organizacionales.
Para que sea aplicable, la Programación Lineal debe reunir los siguientes requisitos:
Para que sea aplicable, la Programación Lineal debe reunir los siguientes requisitos:
- Tiene que optimizarse un objetivo.
- Las variables o fuerzas que afectan los resultados poseen relaciones directas o en línea recta.
- Hay obstáculos o restricciones sobre las relaciones de las variables.
Sin las restricciones de la Programación Lineal incluyen la maximización de la producción, minimizar los costos de distribución y determinar los niveles óptimos del inventario.
